NET Y
 INTRODUCTION “Net Y” is an acronym for Nested Tetrahedrons Y. It
is a two player game. A printed paper “board,” a pen of one color, and a
pen of another color can be used to play. The original game of Y was first
described by Claude Shannon in the early 1950’s, and independently
reinvented around the same time by Craige Schensted and Charles Titus.
Mark Steere created this variant of Y on March 31, 2006. In Net Y, there
are three superimposed, interdependent instances of Y which are played
simultaneously.
INTRODUCTION “Net Y” is an acronym for Nested Tetrahedrons Y. It
is a two player game. A printed paper “board,” a pen of one color, and a
pen of another color can be used to play. The original game of Y was first
described by Claude Shannon in the early 1950’s, and independently
reinvented around the same time by Craige Schensted and Charles Titus.
Mark Steere created this variant of Y on March 31, 2006. In Net Y, there
are three superimposed, interdependent instances of Y which are played
simultaneously.
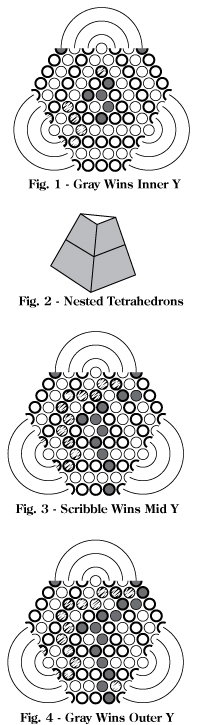
SETUP The board can be viewed as having three “arms” as shown in
Figure 1, with arcs connecting the side edges of the arms. If the arms
were folded out of the page and inward, the tetrahedral shape shown in
Figure 2 would form. The tiny half circles along the side edges of the
arms would come together as indicated by the arcs to form whole circles.
BASIC MOVES Normally two different color pens are used, such as red
and blue - one for each player. Here one player will be Gray and the other
Scribble. Players take turns coloring in circles on the (initially empty)
board, one circle per turn, or two corresponding half circles in a turn.
THREE DIMENSIONAL PERSPECTIVE In three dimensions the
board can be viewed as two nested tetrahedrons, each missing its top
peak, having been severed by a horizontal cut. Each of the two
tetrahedral shapes has a trianglular perimeter on top. These two shapes
and a triangle are superimposed on one another. In two dimensions the
top triangle becomes a broken triangle around the outer perimeter, the
intermediate triangle becomes a broken triangle closer in, and the bottom
triangle remains whole in the center of the board.
OBJECT OF THE GAME The three games of Y, each represented by
its own highlighted triangle, are played simultaneously. The player who
wins the majority of them wins overall. In each game of Y, players
attempt to join the three sides of the given triangle with continuous linked
paths of colored in circles (in the players’ own designated colors). The
sides must be connected by points inside the triangle (as viewed in two
dimensions), including its highlighted perimeter.
In Figure 1 Gray has connected all three sides of the center triangle.
Continuing the same game in Figure 3, Scribble has connected the three
sides of the intermediate triangle. In Figure 4 Gray has claimed victory
in the outermost triangle. Since Gray has won two of the three games of
Y, Gray has won overall.
AUTHOR’S NOTE Feel free to copy, distribute, profit from, or do
whatever you like with this document and the game of Net Y. However
please don’t change the name or the rules, and please attribute
the game to me, Mark Steere. Other games I invented: Quadrature,
Tanbo, Impasse, Byte, Diffusion, Cephalopod, and Box Hex. For
more information see marksteeregames.com.
Copyright (c) March 2006 by Mark Steere
 INTRODUCTION “Net Y” is an acronym for Nested Tetrahedrons Y. It
is a two player game. A printed paper “board,” a pen of one color, and a
pen of another color can be used to play. The original game of Y was first
described by Claude Shannon in the early 1950’s, and independently
reinvented around the same time by Craige Schensted and Charles Titus.
Mark Steere created this variant of Y on March 31, 2006. In Net Y, there
are three superimposed, interdependent instances of Y which are played
simultaneously.
INTRODUCTION “Net Y” is an acronym for Nested Tetrahedrons Y. It
is a two player game. A printed paper “board,” a pen of one color, and a
pen of another color can be used to play. The original game of Y was first
described by Claude Shannon in the early 1950’s, and independently
reinvented around the same time by Craige Schensted and Charles Titus.
Mark Steere created this variant of Y on March 31, 2006. In Net Y, there
are three superimposed, interdependent instances of Y which are played
simultaneously.