HEX KB TOPOLOGY

A Technical Discussion

by Mark Steere

INTRODUCTION

[This document is actually the original version of the Hex KB rule sheet. It goes into a lot more technical detail than does the current version, which technical detail can be off putting to many readers.  The language of this document may differ slightly in meaning from the same language used in the current rule sheet.]

Hex KB is a two player game, played on the grid shown in Figure 1. This grid represents a Klein bottle with a window cut from it. The perimeter of the window is divided into four segments, alternately colored red and blue.

The left edge of the grid connects to the right edge, as with a cylinder. The top edge of the grid connects to the bottom edge in reverse. Numbers on the top scale increase to the right and numbers on the bottom scale increase to the left.

[Technical note: The amount of phase phase shifting used when connecting top to bottom, in this case 180 degrees, is arbitrary. In other words, before connecting the top of the cylinder to the bottom, you can twist the cylinder to any degree. This will have no affect on the topology of the Klein bottle.]


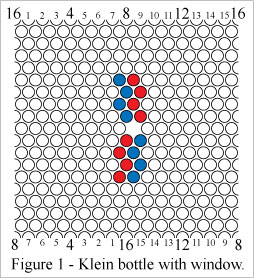
Players take turns adding stones of their own color to the board. Draws cannot occur in Hex KB. Mark Steere designed Hex KB in March 2009.

LOOP TYPES

Four types of loops can be formed on the surface of a Klein bottle, as illustrated in the following diagrams.

Figure 2 shows a "simple loop". A simple loop doesn't wrap around the horizontal axis or the vertical axis.


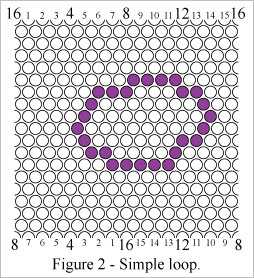
Figure 3 shows a "cylinder loop" which wraps around the cylinder axis (vertical axis here) of the grid.


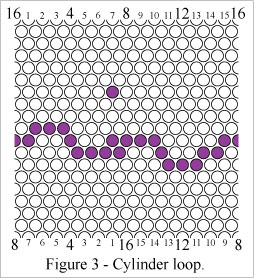
Figure 4 shows a "mobius loop" which wraps around the mobius axis (horizontal axis here) of the grid one time. There can be at most two non-intersecting mobius loops on a Klein bottle.


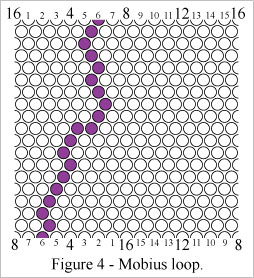
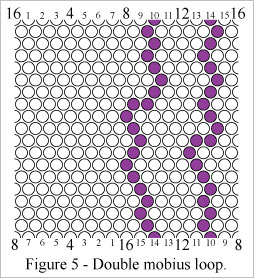
Figure 5 shows a "double mobius loop" which wraps around the mobius (horizontal) axis of the grid twice. A loop can wrap around the mobius axis of a Klein bottle at most two times (without intersecting itself).


Any loop drawn on a Klein bottle can be morphed into one of these four types. And, likewise, the above four loops can be morphed into all possible Klein bottle loops.

[Technical note: As you can see, none of these four loops surround both the horizontal and vertical axes. It isn't possible to change a loop's net number of revolutions around an axis by morphing it. Since all Klein bottle loops are morphs of the above loops, it isn't possible for a loop to wrap around both axes. Loop morphology will be explored in the Morphology section below.]

OBJECT OF THE GAME

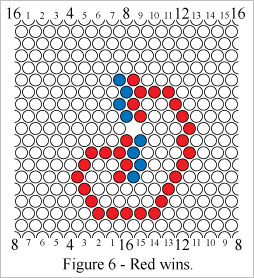
Hex KB can be won in four ways, each of which involves the formation of a "connecting path" - a looping path which connects to the two perimeter segments of its own color. If a connecting path's endpoints were bridged over the window, the resulting loop would be one of the four Klein bottle loop types.

In Figure 6 Red wins by forming a simple connecting path.


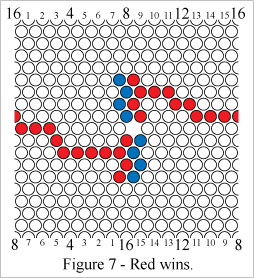
In Figure 7 Red wins by forming a cylinder connecting path.


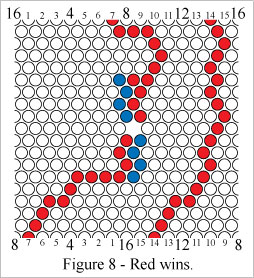
In Figure 8 Red wins by forming a mobius connecting path and a mobius loop. NOTE: Two paths are required in this winning condition.


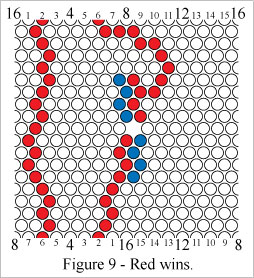
In Figure 9 Red wins by forming a double mobius connecting path.


PERIMETER CELLS

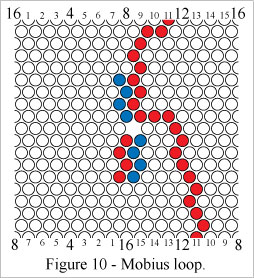
Cells in a perimeter segment can be used as part of a path.

Figure 10 shows a mobius loop which includes perimeter segment cells.


MORPHOLOGY

Cylinder loops can be morphed by dragging points on the left edge of the grid upward or downward, and dragging corresponding points on the right edge up or down the same distance and in the same direction. See Figure 11.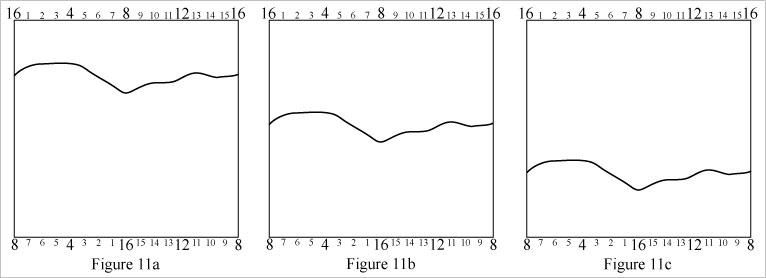


Mobius loops can be morphed by dragging points at the top edge leftward or rightward, and dragging corresponding points on the bottom edge the same distance but in the opposite direction. See Figure 12.


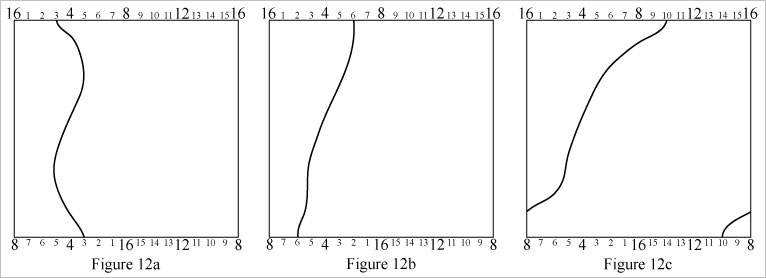
[Technical note: In Figure 12c, the path appears to loop around both axes of the Klein bottle. In fact it does not. The helical appearance of the path is an artifact of modeling a Klein bottle with a square grid. If you follow the path in Figure 12c upward, the path's coordinate on the top edge scale increases (...7, 8, 9, 10). Now if you continue to follow the path up from the bottom of the grid, the path's coordinate on the bottom edge scale decreases (10, 9, 8, 7,...). How much the path winds around the grid on its approach to the top is how much the path unwinds around the grid on its approach from the bottom. The path is winding and unwinding simultaneously. A mobius loop has zero revolutions around the cylinder (vertical) axis and it can't be morphed to have more than zero revolutions around the cylinder axis.]

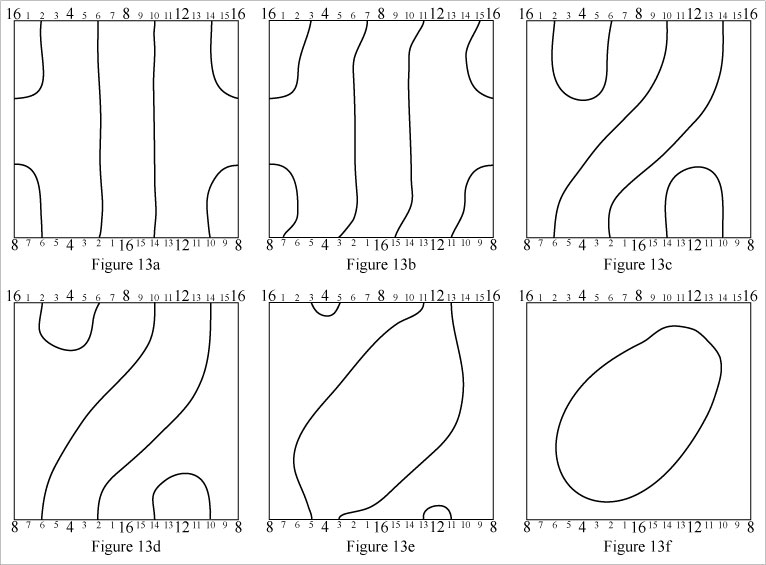
The intricate loop in Figure 13a reduces to the simple loop in Figure 13f.


The loop in Figure 14a appears to be a simple loop, encircling neither of the Klein bottle's axes. In fact it is not. The simple loop appearance is an artifact of representing a Klein bottle with a simple grid. This loop is a cylinder loop as can be seen when it's morphed to the shape in Figure 14f.


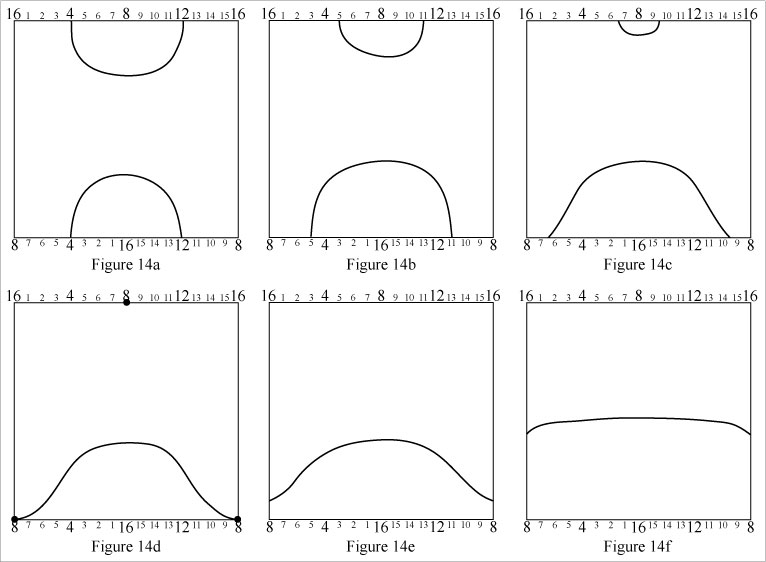
[Technical note: In Figure 14a, following the portion of the path near the top of the grid from left to right, it wraps around half of the cylinder - (4, 5, 6, 7, 8, 9, 10, 11, 12). Continuing from right to left near the bottom of the grid, the path goes on to encircle the remaining half of the grid - (12, 13, 14, 15, 16, 1, 2, 3, 4) - as read from the bottom edge scale. So the loop in 14a is seen to completely encirle the cylinder (vertical) axis, consistent with Figure 14f.]

ALTERNATIVE GRID

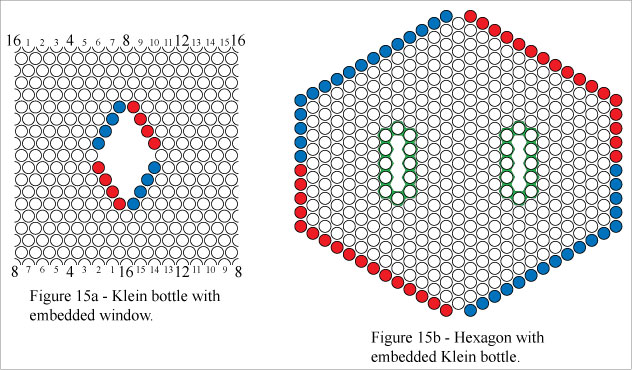
The grid in Figure 15a represents a Klein bottle with a window cut from it. If you take the window and stretch it outward, you get something like the grid in Figure 15b, which has two "portals". The perimeter cells of the portals are highlighted in green.

The portals are considered to be coincident. When a cell in the perimeter of one portal is claimed, the corresponding cell in the perimeter of the other portal is also claimed. See Figures 19b and 20b.


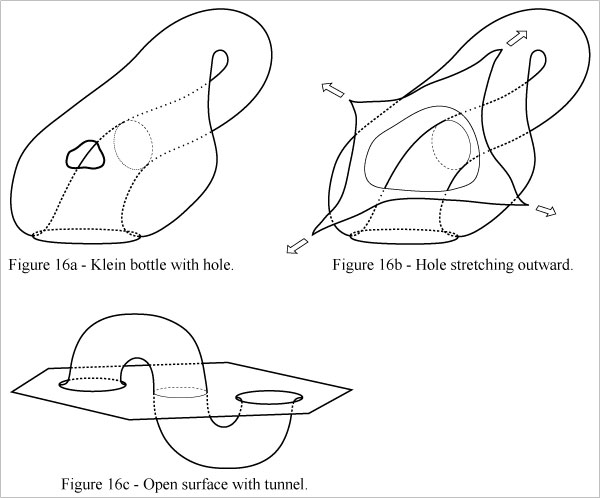
[Technical note: Figure 16 demonstrates the transformation between the two morphs represented in Figure 15. As you can see, the two windows in Figure 15b are connected by an S shaped tunnel. If the tunnel is shortened to length zero, the two windows coincide.]


WIN CONDITIONS ON ALTERNATIVE GRID

In Figures 17a and 17b Red wins by forming a simple connecting path.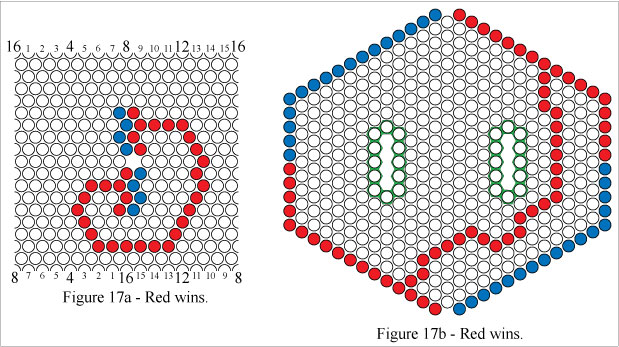


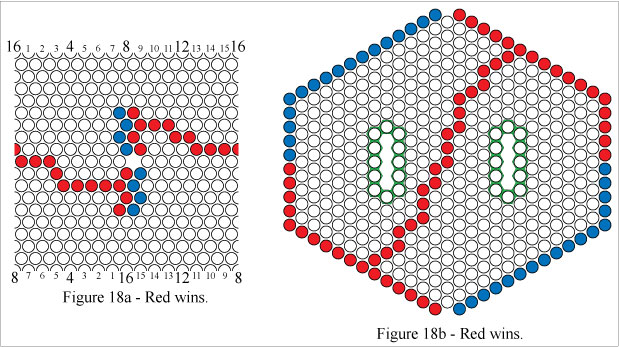
In Figures 18a and 18b Red wins by forming a cylinder connecting path.


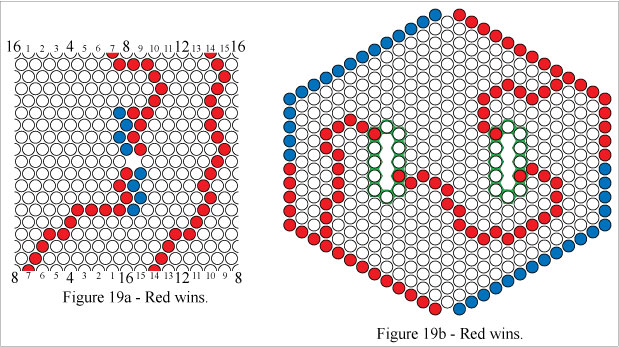
In Figures 19a and 19b Red wins by forming a mobius connecting path and a mobius loop, two separate paths.


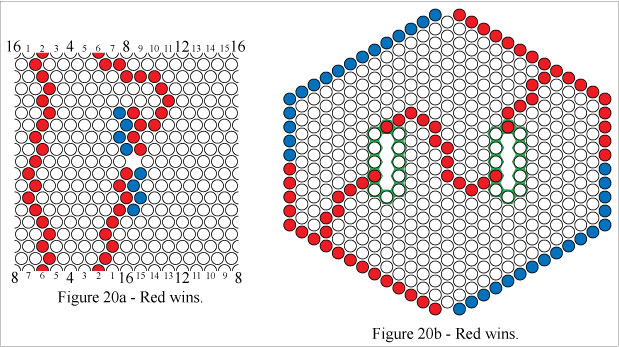
In Figures 20a and 20b Red wins by forming a double mobius connecting path.


PERIMETER CELLS (ALTERNATIVE GRID)

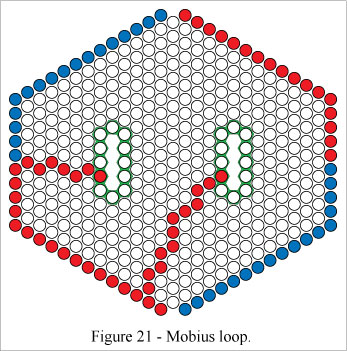
Cells in a perimeter segment can be used as part of a path, just as with the square grid representation.

Figure 21 shows a mobius loop which includes perimeter segment cells.



Copyright (c) March 2009 by Mark Steere